Teruji Thomas | The Asymmetry, Uncertainty, and the Long Term
Presentation given at the Global Priorities Institute
September 2019
TERUJI THOMAS: (00:06) Hi. I'm Teru Thomas from the Global Priorities Institute and I'm going to be talking about a paper I've been working on which will be called something like The Asymmetry, Uncertainty and the Long Term.
- Introduction
So, how bad would it be if life on Earth went extinct let's say within the next century? It could be a huge asteroid that crashes into the Earth and wipes everything out. There are other scenarios having to do with climate change or biotechnology. Lots of scenarios we could consider. I'm going to focus on the impact that extinction would have on people, but of course other things might matter as well.
So one thing that would happen is about eight billion people will be killed. Another thing that would happen though is that there wouldn't be any future people. Now how many future people wouldn't there be? Well, it depends of course, but it's not that hard to tell a story on which there might be 1016 or perhaps vastly more future people if things go smoothly and what's striking is that the second consideration is, at least potentially, a lot more important than the first one. So, going just by total welfare let's say, a one-in-a-million chance of 1016 extra lives might easily be worth all of the welfare of all of the people currently alive. Now, one idea that's popular among economists and pretty unpopular among philosophers is that we should simply exponentially discount the welfare of future generations and that's not a debate I'm going to talk about.
I want to talk about a different idea and the idea is that even though we may very well have an obligation to improve the lives of the present and future people, we simply don’t have a similar obligation or requirement to increase the number of future people for example, by preventing extinction. And more precisely a lot (02:00) of people are, at least initially, attracted to something like the following idea, which is called The Asymmetry. So, suppose we have a choice between on the one hand the status quo, creating no one, and on the other hand creating a lot of people, some additional people, and if we create the additional people that will have no effect on the people who independently exist. Then first of all, if the additional people would certainly have bad lives, we ought not to create them. But second, if the additional people would certainly have good lives, it's permissible but not required to create them. So, if this is right that would mean that the second consideration against extinction would not really be important. It would be the first consideration that would really matter. Now, it may help to say a little bit about the motivation behind this idea. Suppose we create someone who we know will have a bad life, then in some sense that person is our victim. Right? They have a complaint about what we did. On the other hand if in the second case, we simply don’t create someone who would hypothetically have had a good life, then there is no victim and there's no one who has a complaint about what we did. So that's usually how this idea is understood.
Now, the problem is that the Asymmetry is just one principle. It's not a complete theory and there are very few, next to no theories of Asymmetry that are well worked out to the extent that we could do any kind of serious analysis, for example, plugging this theory into an economic model or something like that. And in particular, when we think about any remotely realistic sort of choice it becomes crucial how we think about uncertainty or risk and none of the existing theories of the Asymmetry say anything really about that. So, my main goal here is to get some better theories of the Asymmetry on the table that deal with risk (04:00) in a plausible way and along the way I want to make it clearer what kind of principles we might rely on and what kinds of problems and choice points arise along the way. So first, I'm going to introduce you to some of the problem cases that we can use to guide our thinking about the Asymmetry.
- Problem Cases


In this first case, which I call Mixed Addition, there are two options Act 1 and Act 2 and in all of these examples you should think of Adam as being essentially the current generation and Eve, Cain and Abel are potential future people.
So in the first option, Act 1, Adam alone exists and he has a pretty good life represented by the number 10. In Act 2, we create Eve, Cain and Abel and Eve and Cain also have pretty good lives, but Abel has a slightly bad life represented by minus one (–1). Now, some theories of the Asymmetry are going to say that we ought to choose Act 1. Why is that? Well remember what I was saying just now about the motivation involving victims or complaints. If we look here, Abel has a complaint about Act 2. He has a bad life. However, in Act 1 no one has any complaint. Right? So, on that basis it looks like you ought to choose Act 1 rather than Act 2. And if that's right then there's at least a heuristic here that we want to positively encourage extinction and that's because if we don’t go extinct, then there will inevitably be some bad lives in the future. At least as far as this example goes, it looks like we should prevent those lives from coming into existence. But I don’t think that's really compelling and Joshua Gert has a useful idea here, a distinction between reasons that require us to do something and reasons that merely justify us in doing that thing. And I think it's fairly plausible here that the fact that Eve and Cain would have good lives in (06:00) the second option, even though that can't require us to choose Act 2, it might well justify us in choosing Act 2. The fact that Eve and Cain would have good lives can render Act 2 permissible. Anyway, that's one example to think about.
Here is the second case which has a similar structure.


Here in Act 2 we create Eve, Cain and Abel with good lives, all of them. But this comes at some cost to Adam. He gets nine instead of ten. Now again, if we think about complaints or victims, we can see that Adam has a complaint about Act 2 and no one has a complaint about Act 1. So again, that's how you might argue for a verdict that we ought to choose Act 1 over Act 2. So, even if it's permissible to create future people, it would be impermissible to do so at any cost to the current generation. That's a ‘hard’ verdict, but you might think in light of what I was saying before that in fact the ‘soft’ verdict is the correct one, that in a choice like this either option is permissible. Again after all, if the fact that Eve, Cain and Abel have good live, if that fact can justify us in creating some people with bad lives, then it should also perhaps justify us in imposing some kind of cost on the current generation.
Now we come to a third problem, which is I think [inaudible 07:28]. This is the famous Non-Identity Problem. The Asymmetry is mostly about increasing the numbers of future people, but we should also ask about improving their lives. And there are lots of different things that can fall under the vague heading of ‘improving lives’. So for one thing we can keep the people the same, but make their lives better. That's one way of improving lives. But another thing is to make different people who happen to have better lives and as Derek Parfit influentially argued, in the long run (08:00) we tend to do the latter thing. Most of the things that we do will have some eventually quite wide-ranging effect on the identities of future people.
So for example, consider Case 3.


Here in Act 1, I have Adam, Eve, Cain and Abel. Eve, Cain and Abel have slightly good lives and in Act 2, I replaced them by three different people, Eve’, Cain’ and Abel’. Now, of course if we were going by total welfare, then we ought to choose Act 2 over Act 1. That's what I would call the ‘Wide’ verdict, but if you thought about complaints, you might instead think that you ought to choose Act 1 over Act 2 and that's because, again, Adam has a complaint against Act 2. He's worse off than he could have been. Whereas, when we look at Act 1, no one has any complaints. Adam, Eve, Cain and Abel, they all have good lives and none of them could have been better off. So that's how you would argue for this ‘Narrow’ verdict that you ought to choose Act 1. There's no victim. Okay. So it might look like endorsing this ‘Narrow’ verdict would greatly undermine the importance of improving the lives of future people insofar as these improvements tend to change the identities of future people. Now that is true to some extent but there are some subtleties here.


So in the previous case Eve, Cain and Abel have good lives and there was an option of replacing them with better lives. Here, Eve, Cain and Abel all have slightly bad lives and again we can replace them with different people with good lives. All kinds of views are liable to say that here we ought to choose Act 2 over Act 1 and that's because even though Adam still has a complaint against Act 2, here Eve, Cain and Abel all have complaints against (10:00) Act 1 insofar as they have bad lives and that consideration could easily outweigh Adam’s complaint. Right? So all kinds of views are likely to recognize the importance of some kinds of ways of improving the lives of future people here by replacing bad lives with good ones.
Now, we come to a fourth issue which is the thorniest of all and I don’t have time to say much about it today. And the problem is that the Asymmetry strongly suggests that this relation ‘ought to choose x over y’, the relation between options, is not a transitive relation. And that raises us all kinds of issues related to decision theory.
Now, in the written version of the paper I suggest that one might borrow Condorcet methods from voting theory in order to deal with some of these issues. The idea there is that there are similar, structurally similar kinds of intransitivities that arise in the voting theory from the so-called Condorcet or voting paradox, so there might be some ideas that we can borrow from voting theory there. But today I'm just going to side step all of these issues by focusing on two option choices. Right? For two option choices the issue of intransitivity just doesn’t arise. However, I will note that the standard way of thinking about choice under uncertainty and the expected utility theory does presuppose transitivity and as a result there's not going to be any, at least any completely straightforward application of expected utility theory in the context of the Asymmetry. So how should we think about risky choices? That's what I want to talk about next.
- Risk
Alright. So, the plan here… I'm going to give some general principles that enable us to reduce arbitrary risky choices to risk-free choices. So, given these principles all that remains (12:00) to be done is to write down a theory of the Asymmetry in risk-free cases. I call these principles supervenience principles. Supervenience is a piece of philosophical jargon. All it means here is that these principles specify conditions under which we ought to treat one choice, for example between {A, B}, the same way as the second choice between {C, D}. So what that means is, if we ought to choose A over B, then likewise we ought to choose C over D and if we ought to choose B over A, then likewise we ought to choose D over C. That's what the supervenience principles will do here.
Here is the first one, which I call Personwise Supervenience. It goes like this, and I'll give an example in a minute. Suppose that each person P and each pair of welfare levels x and y, and these can include non-existence, the probability that P would get x under the first option and y under the second option is the same in each of these two choices. So the probability that P would get x under A but y under B is the same as the probability that P would get x under C but y under D. Okay. So if that condition holds, then the principle says that we ought to treat the choice between A and B the same as the choice between C and D. So here's an example. Here's how it works.


Here in the first row I have Acts A and B. So that's the first choice. In the second row I have Acts C and D. That's the second choice. Now when I look here, I'm flipping a fair coin H is heads and T is tails. So the columns here correspond to different outcomes of the coin toss and in Act A, if the coin lands heads then (14:00) Adam gets x, whereas in Act B, if the coin lands heads then Adam gets y. So there's a 50% chance that Adam gets x under the first Act and y under the second Act and similarly a 50% chance that Adam gets z under the first Act and w under the second Act. Now when we look at the choice between C and D, all I've done is I've switched the roles of the two states, heads and tails, from Adam’s point of view. So it's now on tails that he gets either x or y and it's now on heads that he gets either z or w. But it's still true that there's a 50% chance that Adam gets x under the first Act and y under the second and it's still true that there's a 50% chance that Adam gets z under the first Act and w under the second. So the personwise supervenience principle says that switching around the payoffs in these ways makes no difference to which of the two options we ought to choose. Now because people often ask about this let me point out. I'm not saying that if we merely switch around x and z here that that wouldn't make a difference to which option we ought to choose. I'm switching around x and z, but at the same time I'm switching around y and w. So this preserves the point that it's still in the same state here heads and here tails that Adam gets x or y and here's tails where Adam gets x or y. Okay.
The second principle which I call the Statewise Supervenience has a similar flavor. So now suppose that in each state, for example heads or tails, and for each pair of welfare levels the number of people who would get x under the first Act but y (16:00) under the second Act is the same in the two choices, then the principle says that we ought to choose the choice from A and B in the same way as the choice from C and D. Alright. Let me illustrate that again.
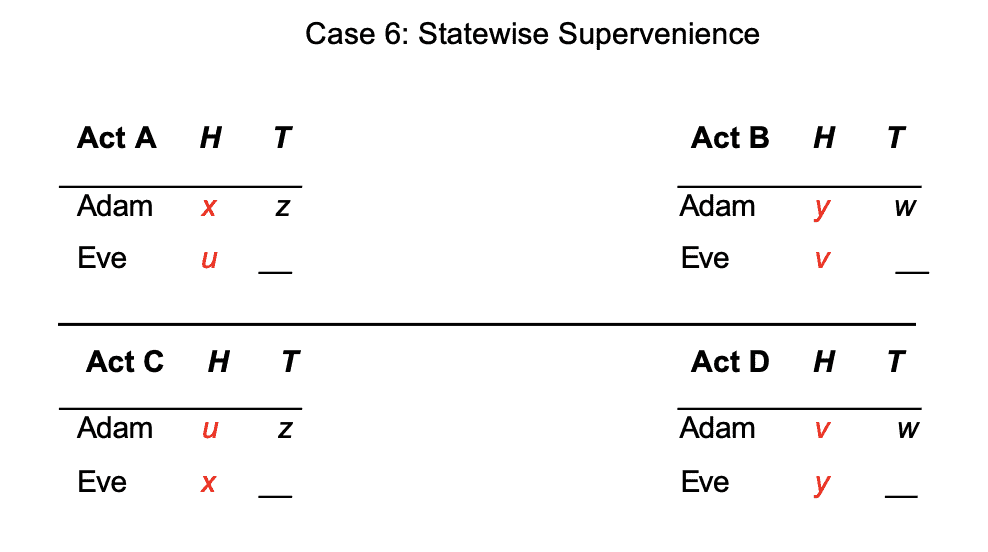

So here I'm focusing on a specific state, heads. So on heads in the first pair of options there's one person who gets x in the first Act rather than y in the second Act and there's one person who gets u in the first Act rather than v in the second Act and down here the choice between C and D, that's still true. I've just switched the roles of the two people. So here there's still one person who gets x rather than y . Now it's Eve rather than Adam and there's still one person who gets u rather than v. Now it's Adam rather than Eve and the statewise supervenience principle says that switching around the payoffs in this way doesn't make any difference to what we ought to choose. Okay.
The third principle is called Scale Invariance and it says this. Suppose that the first choice is just a scaled up version of the second choice and by that I mean it involves more people but they have the same pattern of interests. Then we ought to treat a choice between {A, B} the same way as the choice between {C, D} and that will become clear from this illustration.
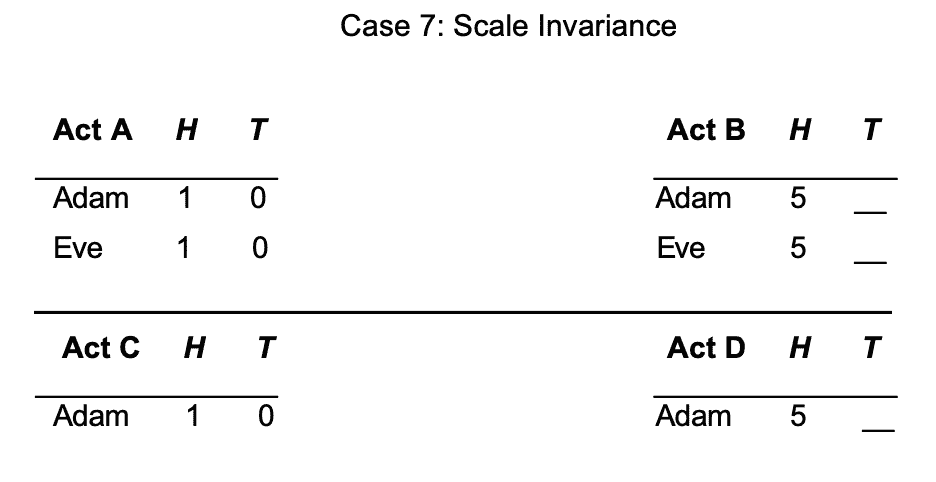

Here when we look at C and D I just have Adam. Okay? And in the first choice between A and B I've introduced Eve who is basically a clone of Adam. Her interests are perfectly aligned with his and that's what I mean by scaling up. Okay? Here they're scaled up by a factor of two but we could scale up by a greater factor as well. And the scale invariance principle says that scaling up in this way makes no difference to which of the two options we ought to choose. Alright.
So there's obviously (18:00) a lot more to say about these three principles to defend them and explain why they might be true, but I have to skip to the main result here which I call the Supervenience Theorem and it says given these three principles that I've just been describing, a theory of risky choices is completely determined by its restriction to risk-free cases. So if I spell out what the theory says in risk-free cases then that will automatically determine what you ought to do in risky cases as well. Alright. So I'm going to start by giving you two basic examples here. These two basic examples have nothing to do with the Asymmetry and then I will sketch out the third example in more detail. So this is just to give you the hang of it.
So suppose that you maximize total welfare in risk-free cases. Alright. Suppose that's your view about risk-free cases. Then the upshot of the theorem is that in risky cases you maximize expected total welfare. So that's a form of Total Utilitarianism. Suppose on the other hand for a second example that you maximize average welfare in risk-free cases. Then the upshot of the theorem is that in risky cases you maximize this ratio expected total welfare divided by the expected number of people. Okay.
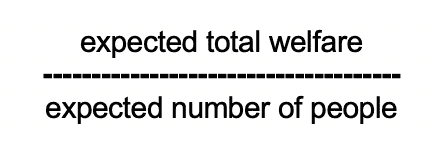
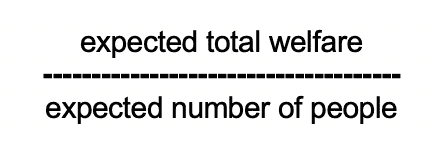
So that's a form of2 Average Utilitarianism. But notice that this thing here, this ratio, isn't the expected average welfare and in fact it's not the expected anything. So this is an example of how these principles are compatible with and even lead to violations of expected utility theory.
- A Theory of the Asymmetry
Now the third thing, the third example I'm going to sketch out how these principles could be combined with a theory of the Asymmetry and I don’t really (20:00) expect you to absorb all of the details here. You have to look at the written version to completely understand what's going on. The main thing that I want to get across is that this is genuinely possible and not altogether difficult. So in thinking this through we should remember some of the choice points that I identified earlier on in the talk. We should think about what to say in costly additional cases. That was the hard/soft distinction in Case 2 and we should think about what to say about non-identity cases that was the narrow/wide distinction in Case 3. And for today I'm going to focus on a ‘wide, hard’ view. That's probably the most popular type of view and remember here that ‘wide’ means that we generally are required to improve lives even in non-identity cases. ‘Hard’ means that we shouldn't do costly addition, that is, we shouldn't create additional people if that imposes a cost on independently existing people. And I'm also going to allow for mixed addition, that is, we are in some cases permitted to create a mixture of good and bad lives if we do so costlessly. That was the first case that I considered. So how would such a view work? Well suppose we're given two outcomes A and B this is the risk-free version, the risk-free outcomes and let's suppose that there are more people in option A. Okay. Or at least as many people, I should say. So what should we think about when making a choice between these two options? First of all we should look at the Necessary people and by that I just mean the people who exist in both of the options. Let's say there's some number of necessary people and they have some total welfare in each of the two options. Then there are the other people the Contingent people, the people who exist only in A or only in B and there's some number of them with some total welfare into the two (22:00) options. Now because I said that there are more people or at least as many people in A, that means that there's some excess number of people in there and of course it's not that some particular people are the excess people. It's just some excess number of people. And there's the natural way of dividing up this total welfare of the contingent people attributing some of it to the excess people in A and the rest of it to the non-excess number of people. So divided up in that way. Then this is the this is how the view goes.


To choose between these two options we should weigh up three things. First of all, the effect upon the necessary people in terms of their total welfare. Second, the effect on the non-excess number of contingent people in terms of their total welfare and third, if the excess people in A would have bad lives, then we want to take that into account as well. Alright. So you just kind of add up those three terms. Now that's the view I said when A and B don't involve any uncertainty.
Now we plug this view into the theorem and it spits out a view of risky choices as well and in fact the general view with risk is formally the same except whenever I talk about the number or the total welfare of necessary or contingent people, we should just use their expected number or their expected total welfare. So it's a fairly straightforward generalization of the original risk-free view. Okay.
- Conclusion
So I wish I had some more time to show you some examples of this theory that I've just sketched in action but I hope I've at least made it to be clearer to you what it might take to write down a theory of variable population, risky choices that's compatible with the Asymmetry. Okay.
So just to recap a bit I'm proposing Supervenience (24:00) principles that allow us to reduce risky choices to risk-free choices. Second, I briefly mentioned the idea of borrowing some Condorcet methods from voting theory in order to deal with intransitivity. And third, given all that all we have to do is write down a theory of risk-free pairwise, that is, two option choices like this ‘wide, hard’ view that I was talking about at the end. I will also draw one relatively practical takeaway of all this. It may seem like the Asymmetry tends to undermine the importance of the long-run future and of course that's true in some sense, but as I suggested, many views are actually going to demand sacrifices on the current generation in order to improve the lives of future people, in particular ways and as I suggested one kind of intervention that will be supported by a great many views would be interventions that are aimed at reducing the number and severity of bad future lives.
Thank you very much.